算法+数据结构=程序
数据结构是底层，算法高层。数据结构为算法提供服务。算法围绕数据结构操作
# 数据结构
# 常见的数据结构
- 数组（Aarray）
- 栈（Stack）
- 链表（Linked List）
- 图（Graph）
- 散列表（Hash）
- 队列（Queue）
- 树（Tree）
- 堆（Heap）
# 数组
几乎所有的编程语言都原生支持数组类型，因为数组是最简单的内存数据结构。JavaScript里也有数组类型，尽管它的第一个版本并没有支持数组。
# 创建和初始化
let daysOfWeek = new Array();
daysOfWeek = new Array(7);
daysOfWeek = new Array('Sunday', 'Monday', 'Tuesday', 'Wednesday',
'Thursday', 'Friday', 'Saturday');
console.log(daysOfWeek.length); //7
# 访问元素和迭代数组
要访问数组里特定位置的元素，可以用中括号
[]传递数值位置，得到想知道的值或者赋新的值。
for (let i = 0; i < daysOfWeek.length; i++) {
console.log(daysOfWeek[i]);
}
# 添加元素
添加到尾部
const numbers = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
numbers[numbers.length] = 10
// or
numbers.push(1,2,3)
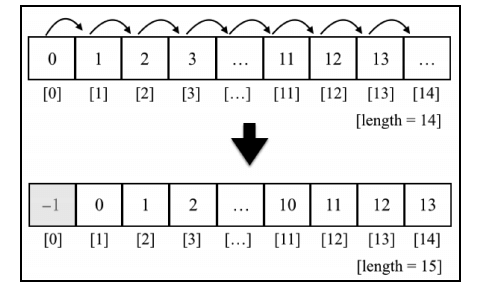
添加到开头
要腾出数组里第一个元素的位置，把所有的元素向右移动一位。我们可以循环数组中的元素，从最后一位（长度值就是数组的末尾位置）开始，将对应的前 一个元素（i-1）的值赋给它（i），依次处理，最后把我们想要的值赋给第一个位置（索引 0）上。
const numbers = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
Array.prototype.insertFirstPosition = function(value) {
for (let i = this.length; i >= 0; i--) {
this[i] = this[i - 1];
}
this[0] = value;
};
numbers.insertFirstPosition(-1);
or
numbers.unshift(-4, -3); //（此方法背后的逻辑和 insertFirstPosition 方法的行为是一样的
# 删除元素
末尾删除元素
const numbers = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
numbers.pop();
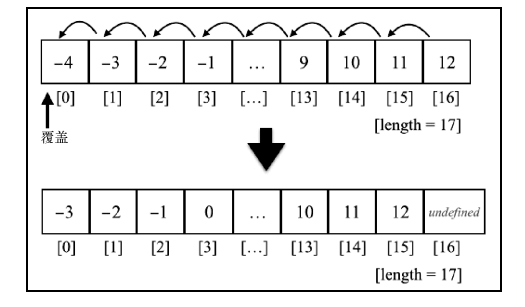
开头删除元素
const numbers = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
for (let i = 0; i < numbers.length; i++) {
numbers[i] = numbers[i + 1];
}
or
numbers.shift();
# 任意位置添加或删除元素
arr.splice(位置，删除元素的个数，要追加的元素); 任意位置添加删除
const numbers = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
numbers.splice(5,3);
# 栈
# 算法
算法是规则的有限集合，是为解决特定问题而规定的一系列操作
# 算法的特性
- 有限性：有限步骤之内正常结束，不能形成无穷循环
- 确定性：算法中的每一个步骤必须有明确的含义，无二义性
- 可行性：原则上能精确进行，操作可通过已实现的基本运算执行有限次而完成
- 输入：有多个或者0个输出
- 输出：有至少一个输出
# 算法的设计要求
正确性、可读性、健壮性(鲁棒性)、高效率和低储存量
# 算法的复杂度
算法的时间复杂度和空间复杂度合称为算法的复杂度。
一个算法的优劣主要从算法的执行时间和所需要占用的存储空间两个方面衡量。
# 时间复杂度
时间频度 一个算法执行所耗费的时间，从理论上是不能算出来的，必须上机运行测试才能知道。但我们不可能也没有必要对每个算法都上机测试，只需知道哪个算法花费的时间多，哪个算法花费的时间少就可以了。并且一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。
常见的算法时间复杂度以及他们在效率上的高低顺序记录：
O(1) 常数阶 < O(logn) 对数阶 < O(n) 线性阶 < O(nlogn) < O(n^2) 平方阶 < O(n^3) < { O(2^n) < O(n!) < O(n^n) }
设计的算法推导出的“大O阶”是大括号中的这几位，就需要重新研究新的算法出来，因为大括号中的这几位即便是在 n 的规模比较小的情况下仍然要耗费大量的时间，算法的时间复杂度大的离谱，基本上就是“不可用状态”。
大O推导法：
- 用常数1取代运行时间中的所有加法常数。
- 在修改后的运行次数函数中，只保留最髙阶项。
- 如果最高阶项存在且不是1,则去除与这个项相乘的常数。
var i=j=x=0, sum = 0, n = 100; //执行1次
for( i = 1; i <= n; i++){
sum = sum + i;
for( j = 1; j <= n; j++){
x++; // 执行n*n次
sum = sum + x;
}
}
console.log('时间复杂度'); //执行1次
//执行总次数 = 1 + (n + 1) + n*(n + 1) + n*n + (n + 1) + 1 = 2n2 + 3n + 3
/*
通过大O推导法得出：
1. 执行总次数 = 2n^2 + 3n + 1
2. 执行总次数 = 2n^2
3. 执行总次数 = n^2
*/
//算法时间复杂度表示为： O( n^2 )
function fun(n){
for (int i = 0; i < n; i++) { //执行n次
for (int j = i; j < n; j++) { //执行次数逐渐递减 (n - 1) + (n - 2)……
printf("Hello World\n");
}
}
}
//执行次数= n + (n - 1) + (n - 2)……+ 1 = n(n + 1) / 2 = n^2 / 2 + n / 2
/*
通过大O推导法得出：
1. 执行总次数 = n^2 / 2 + n / 2
2. 执行总次数 = n^2 / 2
3. 执行总次数 = n^2
*/
//算法时间复杂度表示为： O( n^2 )
算法的时间复杂度和两个因素有关：算法中的最大嵌套循环层数；最内层循环结构中循环的次数。
# 空间复杂度
在写代码时，完全可以用空间来换去时间。
一个程序的空间复杂度是指运行完一个程序所需内存的大小。算法的空间复杂度通过计算算法所需的存储空间实现，算法空间复杂度的计算公式记作:S(n)= O(f(n))，其中，n为问题的规模，f(n)为语句关于n所占存储空间的函数。
算法执行时所需的存储空间包括以下两部分:
- 固定部分。这部分空间的大小与输入/输出的数据的个数、数值无关。主要包括指令空间（即代码空间）、数据空间（常量、简单变量）等所占的空间。这部分属于静态空间。
- 可变空间，这部分空间的主要包括动态分配的空间，以及递归栈所需的空间等。这部分的空间大小与算法有关。
空间复杂度计算方法:
- 忽略常数，用O(1)表示
- 递归算法的空间复杂度=递归深度N*每次递归所要的辅助空间
- 对于单线程来说，递归有运行时堆栈，求的是递归最深的那一次压栈所耗费的空间的个数，因为递归最深的那一次所耗费的空间足以容纳它所有递归过程。
当一个算法的空间复杂度为一个常量，即不随被处理数据量n的大小而改变时，可表示为O(1)；当一个算法的空间复杂度与以2为底的n的对数成正比时，可表示为0(10g2n)；当一个算法的空I司复杂度与n成线性比例关系时，可表示为0(n).若形参为数组，则只需要为它分配一个存储由实参传送来的一个地址指针的空间，即一个机器字长空间；若形参为引用方式，则也只需要为其分配存储一个地址的空间，用它来存储对应实参变量的地址，以便由系统自动引用实参变量。
var a=1;
var b=2;
console.log(a,b);
//空间复杂度O（n）=O（1）；
function fun(n){
k = 10
if n == k{
return n
}else{
return fun(++n)
}
}
//调用fun函数，每次都创建1个变量k。调用n次，空间复杂度O（n*1）=O（n)。
for(var i=0;i<n;i++){
var temp = i;
}
//变量的内存分配发生在定义的时候，因为temp的定义是循环里边，所以是n*O(1)
temp=0;
for(i=0;i<n;i++){
temp = i
}
//temp定义在循环外边，所以是1*O(1)
# 算法性能选择
要节约算法的执行时间往往要以牺牲更多的空间为代价，而为了节省空间可能要消耗更多的计算时间
- 若程序使用次数较少，则力求算法简明易懂
- 对于反复使用的程序，应尽可能选择快速的算法
- 若待解决的问题数据量极大，计算机的存储空间较小，则相应算法主要考虑如何节省空间
# 排序算法
- 十大排序算法总结
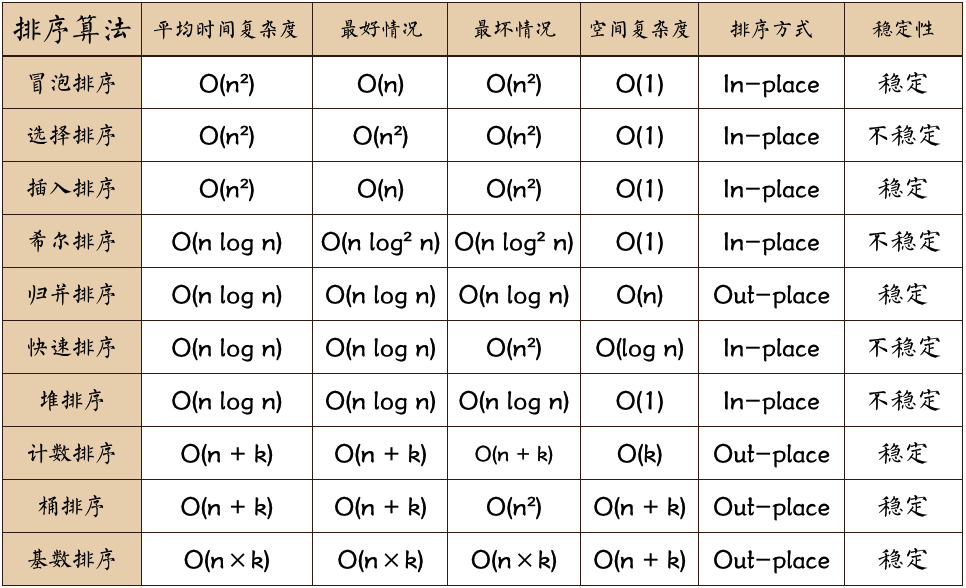https://www.cnblogs.com/jztan/p/5878630.html - 用HTML5实现的各种排序算法的动画比较
http://www.webhek.com/post/comparison-sort.html
# 查找算法
线性查找效率最慢，可对无序列表进行查找、
二分查找效率最快，只能针对有序列表进行查找
# 基于线性表的查找法
- 二分查找(折半查找)
二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。但是，折半查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列。
function binarySearch(data, dest, start, end){
var end = end || data.length - 1,
start = start || 0,
m = Math.floor((start + end) / 2);
if(data[m] == dest){
return m;
}
if(dest < data[m]){
return binarySearch(data, dest, 0, m-1);
}else{
return binarySearch(data, dest, m+1, end);
}
return false;
}
var arr = [-34, 1, 3, 4, 5, 8, 34, 45, 65, 87];
binarySearch(arr,4); //3
# 分块查找法(索引顺序查找)
分块查找是折半查找和顺序查找的一种改进方法，分块查找由于只要求索引表是有序的，对块内节点没有排序要求，因此特别适合于节点动态变化的情况。
# 基于树的查找法
# 二叉排序树(二叉查找树、二叉搜索树)
二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：
- 若左子树不空，则左子树上所有结点的值均小于它的根结点的值；
- 若右子树不空，则右子树上所有结点的值均大于它的根结点的值；
- 左、右子树也分别为二叉排序树；
- 没有键值相等的节点。
# 创建二叉搜索树
function BinaryTree(){
var Node=function(key){ //节点函数
this.key=key;
this.left=null;
this.right=null;
}
var root=null; //根元素
this.insert=function(key){ //对外提供访问函数内部的接口
var newNode=new Node(key);
if(root==null){
root=newNode
}else{
insertNode(root,newNode);
}
}
var insertNode=function(node,newNode){//创建相互关系的根实体
if(node.key>newNode.key){
if(node.left==null){
node.left=newNode;
}else{
insertNode(node.left,newNode)
}
}else{
if(node.right==null){
node.right=newNode
}else{
insertNode(node.right,newNode)
}
}
}
}
二叉树是每个结点最多有两个子树的有序树。
# 二叉树的排序
- 中序遍历
先左后根最后右
var inOrderTraverseNode=function(node,callback){
if(node!=null){
inOrderTraverseNode(node.left,callback)
callback(node.key)
inOrderTraverseNode(node.right,callback)
}
}
this.inOrderTraverse=function(callback){
inOrderTraverseNode(root,callback);
}
- 前序遍历 可以很有效率的复制一个二叉树对象
根节点排最先，然后同级先左后右
var proOrderTraverseNode=function(node,callback){
if(node!=null){
callback(node.key)
proOrderTraverseNode(node.left,callback)
proOrderTraverseNode(node.right,callback)
}
}
//前序遍历 复制 效率高得多
this.proOrderTraverse=function(callback){
proOrderTraverseNode(root,callback);
}
- 后序遍历 选查找子集的特性可以运用在文件系统遍历当中
先左后右最后根
var postOrderTraverseNode=function(node,callback){
if(node!=null){
postOrderTraverseNode(node.left,callback)
postOrderTraverseNode(node.right,callback)
callback(node.key)
}
}
//后续遍历 文件系统遍历
this.postOrderTraverse=function(callback){
postOrderTraverseNode(root,callback);
}
- 测试：
// 前序遍历
var nodes=[8,3,10,1,6,14,4,7,13];
var binaryTree=new BinaryTree();
nodes.forEach(function(key){
binaryTree.insert(key);
})
var callback=function(key){
console.log(key)
}
binaryTree.inOrderTraverse(callback)
# 查找
- 查找指定值
var searchNode=function(node,key){
if(node==null){
return false
}
if(node.key>key){ //小于当前node往左找
searchNode(node.left,key)
}else if(node.key<key){ //大于当前node往右找
searchNode(node.right,key)
}else{ // 找到
return true;
}
}
this.search=function(key){
return searchNode(root,key)
}
- 查找最值
// 最大值
var maxNode=function(node){
if(node){
while(node&&node.right!=null){
node=node.left
}
return node.key;
}
}
this.max=function(){
return maxNode(root)
}
// 最小值
var minNode=function(node){
if(node){
while(node&&node.left!=null){
node=node.left
}
return node.key;
}
}
this.min=function(){
return minNode(root)
}
# 计算式查找法————哈希法
根据关键字（key)而直接访问在内存储存位置
# 简单算法题
- 给定一个包含非负整数的mxn网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。
说明：每次只能向下或者向右移动一步。
输入: [ [1,3,1], [1,5,1], [4,2,1] ] 输出: 7 解释: 因为路径 1→3→1→1→1 的总和最小。
var minPathSum = function(grid) {
var n = grid.length
if(n == 0) return 0
for(let i = 0; i < n; i++){
for(let j = 0; j < grid[i].length; j++){
if(!i && !j) continue
grid[i][j] = Math.min((i ? grid[i - 1][j] : Number.MAX_VALUE),(j ? grid[i][j - 1] : Number.MAX_VALUE)) + grid[i][j]
}
}
return grid[n - 1][grid[0].length - 1]
};
- 给定一个由整数组成的非空数组所表示的非负整数，在该数的基础上加一。
最高位数字存放在数组的首位， 数组中每个元素只存储一个数字。
你可以假设除了整数 0 之外，这个整数不会以零开头。 - 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？ 注意：给定 n 是一个正整数。
示例 1：
输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例 2：
输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
- 给定一个 m x n 的矩阵，如果一个元素为 0，则将其所在行和列的所有元素都设为 0。
输入:
[
[1,1,1],
[1,0,1],
[1,1,1]
]
输出:
[
[1,0,1],
[0,0,0],
[1,0,1]
]
var setZeroes = function(matrix) {
const cached = [];
const a = matrix.length;
const b = matrix[0].length;
for (const i of matrix.keys()) {
for (const j of matrix[i].keys()) {
if(matrix[i][j] === 0) {
cached.push(
...Array(b).fill().map((_, k) => [i, k]),
...Array(a).fill().map((_, k) => [k, j]),
);
}
}
}
for (const [x, y] of cached) {
matrix[x][y] = 0;
}
return matrix;
};
- 给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。
输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
var combine = function(n, k) {
const arr = Array(n).fill().map((_,index) => index + 1);
const buffer = [];
const result = [];
const backTrace = (index, target) => {
if(target == 0) {
return result.push(buffer.slice());
}
if(index === arr.length) return;
buffer.push(arr[index]);
backTrace(index + 1, target - 1);
buffer.pop();
backTrace(index + 1, target);
}
backTrace(0, k);
return result;
};
- 给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数，使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。
例如，给定数组 nums = [-1，2，1，-4], 和 target = 1.
与 target 最接近的三个数的和为 2. (-1 + 2 + 1 = 2).
var threeSumClosest = function(nums, target) {
nums.sort(function(a, b) {
return a - b
})
let res = nums[0] + nums[1] + nums[2]
let cur = 0
let diff = Math.abs(nums[0] + nums[1] + nums[2] -target)
for(let i=0;i<nums.length - 2; i++) {
let j = i + 1
let k = nums.length - 1
while(j<k) {
cur = nums[i] + nums[j] + nums[k]
if(Math.abs(cur - target) < diff) {
diff = Math.abs(cur - target)
res = cur
}
if(cur < target) {
j++
} else {
k--
}
}
}
return res
};
- 给定一个仅包含 0 和 1 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。
输入:
[
["1","0","1","0","0"],
["1","0","1","1","1"],
["1","1","1","1","1"],
["1","0","0","1","0"]
]
输出: 6
- 小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为“根”。 除了“根”之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫，房屋将自动报警。
计算在不触动警报的情况下，小偷一晚能够盗取的最高金额。
输入: [3,4,5,1,3,null,1]
3
/ \
4 5
/ \ \
1 3 1
输出: 9
解释: 小偷一晚能够盗取的最高金额 = 4 + 5 = 9.
输入: [3,2,3,null,3,null,1]
3
/ \
2 3
\ \
3 1
输出: 7
解释: 小偷一晚能够盗取的最高金额 = 3 + 3 + 1 = 7.
- 给定一个赎金信 (ransom) 字符串和一个杂志(magazine)字符串，判断第一个字符串ransom能不能由第二个字符串magazines里面的字符构成。如果可以构成，返回 true ；否则返回 false。
(题目说明：为了不暴露赎金信字迹，要从杂志上搜索各个需要的字母，组成单词来表达意思。)
你可以假设两个字符串均只含有小写字母。
canConstruct("a", "b") -> false
canConstruct("aa", "ab") -> false
canConstruct("aa", "aab") -> true
- 使用栈实现队列的下列操作：
push(x) -- 将一个元素放入队列的尾部。
pop() -- 从队列首部移除元素。
peek() -- 返回队列首部的元素。
empty() -- 返回队列是否为空。
MyQueue queue = new MyQueue();
queue.push(1);
queue.push(2);
queue.peek(); // 返回 1
queue.pop(); // 返回 1
queue.empty(); // 返回 false
/**
* Initialize your data structure here.
*/
var MyQueue = function() {
this.input = []
this.output = []
this.size = 0
};
/**
* Push element x to the back of queue.
* @param {number} x
* @return {void}
*/
MyQueue.prototype.push = function(x) {
this.input.push(x)
this.size += 1
};
/**
* Removes the element from in front of queue and returns that element.
* @return {number}
*/
MyQueue.prototype.pop = function() {
if(this.output.length === 0) {
for(var i = 0; i < this.size; i++) {
this.output[this.size-i-1] = this.input[i]
}
this.size = 0
this.input = []
}
return this.output.pop()
};
/**
* Get the front element.
* @return {number}
*/
MyQueue.prototype.peek = function() {
if(this.output.length === 0) {
for(var i = 0; i < this.size; i++) {
this.output[this.size-i-1] = this.input[i]
}
this.size = 0
this.input = []
}
return this.output[this.output.length - 1]
};
/**
* Returns whether the queue is empty.
* @return {boolean}
*/
MyQueue.prototype.empty = function() {
return (this.output.length===0&&this.size===0)
};
/**
* Your MyQueue object will be instantiated and called as such:
* var obj = Object.create(MyQueue).createNew()
* obj.push(x)
* var param_2 = obj.pop()
* var param_3 = obj.peek()
* var param_4 = obj.empty()
*/
- 给定一个非负索引 k，其中 k ≤ 33，返回杨辉三角的第 k 行。
在杨辉三角中，每个数是它左上方和右上方的数的和。
输入: 3
输出: [1,3,3,1]
var getRow = function(numRows) {
if (numRows === 0) return [1];
const result = [[1]];
for (let index = 1; index < numRows + 1; index++) {
const last = result[result.length - 1];
result.push(Array(index + 1).fill(1).map((_, ind) => (last[ind] || 0) + (last[ind - 1] || 0)))
}
return result[numRows];
};
- 优势洗牌 (田忌赛马)
给定两个大小相等的数组 A 和 B，A 相对于 B 的优势可以用满足 A[i] > B[i]的索引i的数目来描述。
返回 A 的任意排列，使其相对于 B 的优势最大化。
输入：A = [2,7,11,15], B = [1,10,4,11]
输出：[2,11,7,15]
输入：A = [12,24,8,32], B = [13,25,32,11]
输出：[24,32,8,12]
var advantageCount = function(A, B) {
var arr = [];
A.sort(function(a, b) {
return a - b;
});
B.forEach(function(item) {
var index = A.findIndex(function(_item) {
return _item > item;
});
if (index > -1) {
arr.push(A.splice(index, 1)[0]);
} else {
arr.push(A.splice(0, 1)[0]);
} });
return arr;
};
- 给定两个二叉树，编写一个函数来检验它们是否相同。 如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。
输入: 1 1
/ \ / \
2 3 2 3
[1,2,3], [1,2,3]
输出: true
输入: 1 1
/ \
2 2
[1,2], [1,null,2]
输出: false
输入: 1 1
/ \ / \
2 1 1 2
[1,2,1], [1,1,2]
输出: false
var isSameTree = function(p, q) {
const queue = [[p, q]];
while(queue.length) {
const [cp, cq] = queue.shift();
if(!cp && !cq) continue;
if(!cp && cq || cp && !cq) {
return false;
}
if(cp.val !== cq.val) {
return false;
}
queue.push([cp.left, cq.left], [cp.right, cq.right])
}
return true;
};
- 给定一个二叉树，判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征：
节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
输入:
2
/ \
1 3
输出: true
输入:
5
/ \
1 4
/ \
3 6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
根节点的值为 5 ，但是其右子节点值为 4 。
var inorderTraversal = function(root) {
const result = [];
const inorder = node => {
if(!node) return;
inorder(node.left);
result.push(node.val);
inorder(node.right);
}
inorder(root);
return result;
};
var isValidBST = function(root) {
const arr = inorderTraversal(root);
return arr.every((item, index) => item > (index > 0 ? arr[index - 1] : -Infinity));
};
- 给定一个整数 n，求以 1 ... n 为节点组成的二叉搜索树有多少种？
输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3